Modus Berita: Matematika

Tampilkan postingan dengan label Matematika. Tampilkan semua postingan

Selasa, 27 Desember 2011

Trigonometri Kelas 10

Berikut ringkasan materi trigonometri kelas 10 :

Radians - an Alternative Measure for Angle

In science and engineering, radians are much more convenient (and common) than degrees. A radian is defined as the angle between 2 radii (radiuses) of a circle where the arc between them has length of one radius.
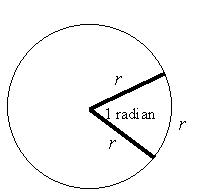
Another way of putting it is: "a radian is the angle subtended by an arc of length r (the radius)".
One radian is about 57.
Radians are especially useful in calculus where we want to interchange angles and other quantities (e.g. length). For example, see how radians are required in Fourier Series. That stuff won't work if we try to use degrees.

Most computer programs use radians as the default.
Care with your calculator! Make sure your calculator is set to radians when you are making radian calculations.
Also, see this simple introduction to radians with an interactive graph.

Converting Degrees to Radians

Because the circumference of a circle is given by C = 2πr and one revolution of a circle is 360°, it follows that:

2π radians = 360°.

This gives us the important result:

π radians = 180°

From this we can convert:

radians → degrees and

degrees → radians.

PENJUMLAHAN DUA SUDUT (a + b)

sin(a + b) = sin a cos b + cos a sin b
cos(a + b) = cos a cos b - sin a sin b
tg(a + b )   = tg a + tg b
                 1 - tg²a

SELISIH DUA SUDUT (a - b)

sin(a - b) = sin a cos b - cos a sin b
cos(a - b) = cos a cos b + sin a sin b
tg(a - b )   = tg a - tg b
                 1 + tg²a

SUDUT RANGKAP

sin 2a = 2 sin a cos a
cos 2a = cos²a - sin² a

= 2 cos²a - 1

= 1 - 2 sin²a
tg 2a = 2 tg 2a
1 - tg²a
sin a cos a = ½ sin 2a
cos²a = ½(1 + cos 2a)
sin2a = ½ (1 - cos 2a)

Secara umum :

sin na = 2 sin ½na cos ½na
cos na = cos² ½na - 1

= 2 cos² ½na - 1

= 1 - 2 sin²½na
tg na =   2 tg ½na
           1 - tg² ½na

JUMLAH SELISIH DUA FUNGSI YANG SENAMA

BENTUK PENJUMLAHAN ® PERKALIAN

sin a + sin b   = 2 sin a + b    cos a - b
                                2              2
sin a - sin b   = 2 cos a + b    sin a - b
                                2             2
cos a + cos b = 2 cos a + b    cos a - b
                                 2              2
cos a + cos b = - 2 sin a + b   sin a - b
                                  2             2

BENTUK PERKALIAN ® PENJUMLAHAN

2 sin a cos b = sin (a + b) + sin (a - b)
2 cos a sin b = sin (a + b) - sin (a - b)
2 cos a cos b = cos (a + b) + cos (a - b)
- 2 sin a cos b = cos (a + b) - sin (a - b)

PENJUMLAHAN FUNGSI YANG BERBEDA

Bentuk a cos x + b sin x

Merubah bentuk a cos x + b sin x ke dalam bentuk K cos (x - a)

a cos x + b sin x = K cos (x-a)

dengan :
K = Öa² + b² dan tg a = b/a Þ a = ... ?

Kuadran dari a ditentukan oleh kombinasi tanda a dan b sebagai berikut

	I	II	III	IV
a	+	-	-	+
b	+	+	-	-

keterangan :
a = koefisien cos x
b = koefisien sin x

Sumber : http://bebas.ui.ac.id/v12/sponsor/Sponsor-Pendamping/Praweda/Matematika/0430%20Mat%203-1g.htm

http://www.intmath.com/trigonometric-functions/7-radians.php

Sabtu, 24 Desember 2011

Penjumlahan Dan Pengurangan Kilat

1. Menentukan jumlah deret bilangan asli

Cara I

Rumus : ½ (n)x(n+1), n= banyak deret

Contoh

a. 1+2+3+4

(banyak deret ada 4), maka

½ (4) (5) = ½ (20) = 10

b. 1+2+3+4+5+6

(banyak deret ada 6), maka

½ (6) (7) = ½ (42) = 21

Cara II

Rumus : n x (n+1) : 2, n=bilangan terakhir

a. 1+2+3+4

Bilangan terakhir 4, maka (4×5):2 = 10

b. 1+2+3+4+5+6

Bilangan terakhir 6, maka (6×7):2 = 21

2. Menentukan jumlah deret bilangan genap

Rumus : n x (n+1) , n = banyak deret bil. genap

Contoh

a. 2+4+6+8

Banyak deret ada 4, maka 4 x (4+1) = 4×5= 20

b. 2+4+6+8+10+12

Banyak deret ada 6, maka 6 x (6+1) = 6×7= 42

3. Menentukan jumlah deret bilangan ganjil

Rumus : n² , n = banyak deret bil. ganjil

a. 1+3+5

Banyak deret ada 3, maka 3² = 9

b. 1+3+5+7+9

Banyak deret ada 5, maka 5² = 25

4. Menentukan hasil pangkat dua bilangan dengan satuan 5

Cara I

Rums : [(n-5) (n+5)] + 5², n=bilangan berpangkat 2

Contoh

a. 15² = [(15-5) x (15+5)] + 5² = [10 x 20]+25 = 225

b. 25²= [(25-5) x (25+5)] + 5² = [20 x 30]+25 = 625

Cara II

Rumus : n (n+1) dan 25,

n= bilangan depan (satuan, puluhan, …)

Contoh

a. 15² = 1 X (1+1) = 2 dan 25 = 2 25

b. 25²= 2 X (2+1) = 6 dan 25 = 6 25

c. 125²= 12 X (12+1) = 156 dan 25 = 156 25 = 15.625

5. Menentukan hasil pengurangan bilangan berpangkat 2

Syarat :

Selisih angka harus 1 dan bilangan pengurang lebih kecil.

Rumus : n1 + n2, n1= bil. terkurang dan n2 bil. pengurang

Contoh

a. 5²-4²= 5 + 4 = 9

b. 25²-24²= 25 + 24= 49

Selasa, 20 Desember 2011

Kumpulan Soal Matematika Kelas 9 Semester 2

Matematika

Download File >>> 100 soal matematika sma kls x semester 2

SAYA AKAN BERIKAN SKKD UNTUK SMA SEKALIAN BAGI YANG SUDAH PADA TINGKAT SMA

Kelas IX, Semester 1

Standar Kompetensi	Kompetensi Dasar
Geometri dan Pengukuran1. Memahami kesebangunan bangun datar dan penggunaannya dalam pemecahan masalah	1.1 Mengidentifikasi bangun-bangun datar yang sebangun dan kongruen1.2 Mengidentifikasi sifat-sifat dua segitiga sebangun dan kongruen 1.3 Menggunakan konsep kesebangunan segitiga dalam pemecahan masalah
2. Memahami sifat-sifat tabung, kerucut dan bola, serta menentukan ukurannya	2.1 Mengidentifikasi unsur-unsur tabung, kerucut dan bola2.2 Menghitung luas selimut dan volume tabung, kerucut dan bola2.3 Memecahkan masalah yang berkaitan dengan tabung, kerucut dan bola
Statistika dan Peluang3. Melakukan pengolahan dan penyajian data	3.1 Menentukan rata-rata, median, dan modus data tunggal serta penafsirannya3.2 Menyajikan data dalam bentuk tabel dan diagram batang, garis, dan lingkaran
4. Memahami peluang kejadian sederhana	4.1 Menentukan ruang sampel suatu percobaan4.2 Menentukan peluang suatu kejadian sederhana

Kelas IX, Semester 2

Standar Kompetensi	Kompetensi Dasar
Bilangan5. Memahami sifat-sifat bilangan berpangkat dan bentuk akar serta penggunaannya dalam pemecahan masalah sederhana	5.1 Mengidentifikasi sifat-sifat bilangan berpangkat dan bentuk akar5.2 Melakukan operasi aljabar yang melibatkan bilangan berpangkat bulat dan bentuk akar 5.3 Memecahkan masalah sederhana yang berkaitan dengan bilangan berpangkat dan bentuk akar
6. Memahami barisan dan deret bilangan serta penggunaannya dalam pemecahan masalah	6.1 Menentukan pola barisan bilangan sederhana6.2 Menentukan suku ke-nbarisan aritmatika dan barisan geometri6.3 Menentukan jumlah n suku pertama deret aritmatika dan deret geometri 6.4 Memecahkan masalah yang berkaitan dengan barisan dan deret

Minggu, 14 Agustus 2011

Logaritma SMA Kelas 10 (X)

Hai teman, sekarang tulisanku ini tentang pelajaran matematika yaitu logaritma dan perpangkatan. Aku ingat dulu pertama kali mendapat pelajaran logaritma adalah kelas 3 SMP. Apakah sekarang masih tetap atau sudah dimulai sejak awal-awal SMP ? Kan biasanya kurikulum di sini cenderung dimajukan ..

Dulu aku butuh waktu yang lama untuk memahami logaritma, hehe maklum, otak pas-pasan

. Mana pangkat masih belum paham banget lagi, udahlah pas ulangan jeblok

, jadi curhat gini .. maap-maap .. langsung saja ya ke pelajarannya.
Logaritma sebetulnya adalah bentuk lain dari pangkat. Kalau kalian ingin mengerti logaritma kalian harus paham dulu soal perpangkatan. Kalau belum paham perpangkatan disini akan aku jelaskan sedikit untuk membantu kalian.
Bentuk pangkat adalah seperti ini : 2³= 8
artinya, 2 X 2 X 2 = 8
lihat angka 2 nya ada 3 kan, makanya disingkat jadi 2³
nah dari situ kita buat rumus umum, a^b= c , artinya a pangkat b sama dengan c.
Lalu bagaimana dengan logaritmanya ? Seperti aku bilang tadi, logaritma adalah bentuk lain dari pangkat. Jika kita punya rumus 2³= 8 , maka bentuk logaritmanya adalah ²log 8 = 3. Atau bila dibuat rumus umum maka akan seperti ini,

^alog c = b

Jika kalian sudah melihatnya polanya maka logaritma akan menjadi mudah, lalu apa sebenarnya polanya? Sebenarnya yang dicari dalam logaritma adalah pangkatnya, bukan seperti pangkat biasa yang mencari hasil dari pangkatnya. Lihat perbedaannya berikut ini,

^alog c = b dan a^b= c

Jelas bukan? Kalau sudah jelas maka berikut ini adalah contoh-contoh dari pangkat dan logaritma.
1. 2³= 8, dan ²log 8 = 3.
2. 5⁵= 625, dan ⁵log 625 = 5.
3. 10⁴= 10000, dan ¹⁰log 10000 = 4.
4. 9² = 81, dan ⁹log 81 = 2.
5. 7⁹ = 40353607, dan ⁷log 40353607 = 9.
Nah, pasti kalian sekarang telah mendapatkan gambaran yang lebih jelas lagi tentang logaritma bukan ?
********** Operasi penyederhanaan logaritma **********
Bagian ini dapat kamu pelajari setelah kamu mengerti penjelasan diatas. Bagian ini adalah bentuk-bentuk logaritma yang dapat digunakan untuk memudahkan kita memecahkan suatu soal. Bentuk-bentuk ini mau tak mau harus dihapal, namun jangan takut karena bentuknya sederhana kok. Lihat bentuk-bentuk penyederhanaan dari logaritma dibawah ini,
1. ^alog (c x d) = ^alog c + ^alog d
contoh: ²log (8) = ²log (2 x 4) = ²log 2 + ²log 4 = 1 + 2 = 3
2. ^alog (c : d) = ^alog c - ^alog d
contoh: ³log (9) = ³log (27 : 3) = ³log 27 - ³log 3 = 3 - 1 = 2
3. ^alog c^d = d x (^alog c)
contoh: ²log 2⁸ = 8 x (²log 2) = 8 x 1 = 8
4. (^alog b)(^blog c) = ^alog c
contoh: (²log 65)(⁶⁵log 8 ) = ²log 8 = 3
5. (^alog b) : (^alog c) = ^clog b
contoh: (⁷log 64) : (⁷log 2) = ²log 64 = 6
**********************************************************
Apabila kalian menemukan bentuk logaritma seperti ini, log x , itu sama artinya dengan ¹⁰log x. Jadi log 100 = … Hayo tebak brapa?

Sumber : http://klikbelajar.com/pelajaran-sekolah/pelajaran-matematika/belajar-matematika-logaritma-dan-pangkat-eksponensial/

Senin, 01 Agustus 2011

Bilangan Berpangkat Kelas 10 (X) SMA

Sudahkah hafal bilangan berpangkat??? taukah kalian tentang definisi bilangan berpangkat??
Yuuuk kita pelajari disini….
Bilangan berpangkat yang paling kita hafal adalah bilangan berpangkat dua dan berpangkat tiga, nah…untuk mempelajari materi-materi lanjutan, baik materi bilangan pangkat bulat positif, bilangan bulat negatif maupun bilangan berpangkat pecahan(akar), kita harus tau lebih dalam tentang definisi perpangkatan itu sendiri !

Let’s check this out …

Pangkat Bulat Positif

$a^n=\underset{sebanyak\;\; n}{a\times a\times a\times...\times a\times a}$

contoh :
1. $10^2=10\times 10=100$

2. $3^3=3\times 3\times3= 27$

3. $(-5)^4=(-5)\times (-5)\times (-5)\times (-5)= 625$

Pangkat Bulat Negatif

$\begin{align*}a^{-n} & = & \frac{1}{a^n}\\ & = & \underset{sebanyak\;\; n}{\frac 1a\times \frac 1a\times \frac 1a\times...\times \frac 1a} \end{align*}$

Contoh :
1. $2^{-5}=\frac{1}{2^5}=\frac 12\times \frac 12\times \frac 12\times \frac 12\times \frac 12=\frac{1}{32}$

2. $(-3)^{-3}=\frac{1}{(-3)^3}=\frac {1}{-3}\times \frac{1}{-3}\times \frac{1}{-3}=-\;\frac{1}{27}$

3. $\frac{1}{10000}=\frac{1}{10^4}=10^{-4}$

4. $7a^{-5}=7.\frac{1}{a^5}=\frac{7}{a^5}$

hmmmmm…..kalau sudah tahu prinsip perpangkatan, coba bikin tabel perpangkatan supaya mudah dalam menghafal,ok..???!!
Sekarang kita lihat aturan dalam perpangkatan yuuuuuuk…

Aturan Pangkat

$a^0=1$

$a^n.a^m=a^{n+m}$

$\frac{a^n}{a^m}=a^{n-m}$

$(a^n)^m=a^{n.m}$

$(a.b)^n=a^n.b^n$

$\left ( \frac ab \right )^n=\frac{a^n}{b^n}$

Mari kita lihat contoh berikut ini….
1. $2^3.2^2=2^5=32$

2. $\frac{5^6}{5^{10}}=5^{-4}=\frac{1}{625}$

3. $(2^2)^3=2^6=64$

4. $(-2a)^3=(-2)^3.a^3=-8a^3$

5. $\left (\frac 5q \right )^3=\frac{5^3}{q^3}=\frac{125}{q^3}$

Contoh soal-soal dan pembahasan aturan pangkat mari kita simak yang berikut ini :
Nyatakan dalam bentuk pangkat positif yang paling sederhana !!!!!

$\begin{align*}1.\;\;(-5a^{-2}b^3)^2&=&(-5)^2(a^{-2})^2(b^3)^2\\&=&25a^{-4}b^6\\&=&\frac{25b^6}{a^4}\end{align*}$

$\begin{align*}2.\;\left (\frac{2}{a^3} \right )^{-4} & = & \frac{1}{\left (\frac{2}{a^3} \right )^{4}}\\ & = & \left ( \frac{a^3}{2} \right )^4\\ & = & \frac{a^{12}}{2^4}\\ & = & \frac{a^{12}]}{16}\end{align*}$

$\begin{align*}3.\;\;\frac{3p^2q^{-5}}{ab^4}\times \frac{a^3b^{-2}}{12p^{-3}q^7}&=&\frac{3{\color{Red} a^3}{\color{DarkBlue} b^{-2}}{\color{DarkGreen} p^2}{\color{Purple} q^{-5}}}{12{\color{Red} a}{\color{DarkBlue} b^4}{\color{DarkGreen} p^{-3}}{\color{Purple} q^7}}\\&=&\frac 14.{\color{Red} a}^{3-1}.{\color{DarkBlue} b}^{-2-4}.{\color{DarkGreen} p}^{2-(-3)}.{\color{Purple} q}^{-5-7}\\&=&\frac 14.a^2.b^{-6}.p^5.q^{-12}\\&=&\frac{a^2p^5}{4b^6q^{12}}\end{align*}$

Latihan yang lain, jangan sungkan-sungkan untuk mencoba yaaaaaa….

cayoooooo…

Sumber : http://www.meetmath.com/311122-materi-bilangan-pangkat.html

Senin, 04 Juli 2011

Konsep Fungsi

Fungsi merupakan objek mendasar yang dihadapi dalam Kalkulus. Konsep fungsi yang abstrak ini akan menyiapkan mahasiswa dalam kuliah kalkulus dengan cara mengkaji gagasan dasar mengenai fungsi, grafiknya serta cara mentransformasikan dan menggabungkan mereka.

Pengertian Fungsi
Bayangkanlah suatu fungsi sebagai sebuah senapan. Fungsi ini mengambil amunisi dari suatu himpunan yang dinamakan daerah asal (daerah definisi atau domain) dan menembakkannya pada suatu himpunan sasaran. Setiap peluru mengenai sebuah titik sasaran tunggal, tetapi dapat terjadi bahwa beberapa peluru mendarat pada titik yang sama. Kita dapat menyatakan definisi secara lebih formal dan memperkenalkan beberapa cara penulisan secara bersamaan.

Klasifikasi Fungsi
Fungsi-fungsi yang akan dibahas dalam diktat ini dapat dikelompokkan ke dalam dua kelompok fungsi, yaitu Fungsi Aljabar dan Fungsi Transenden. Berikut ini akan diberikan fungsi-fungsi aljabar yang penting.

Fungsi Konstan
Fungsi yang berbentuk

dengan

suatu konstanta disebut fungsi konstan. Grafiknya berupa sebuah garis mendatar.

Fungsi Identitas
Fungsi yang berbentuk

disebut fungsi identitas.

Fungsi Polinomial
Fungsi polinomialf dinyatakan sebagai

dengan n bilangan bulat taknegatif, dan

adalah konstanta bilangan nyata (real) dan disebut koefisien polinomial. Jika

maka n disebut derajat dari fungsi polinomial. Pada umumnya daerah asal dan wilayah fungsi polinomial adalah:

dan

dengan

Fungsi Rasional
Fungsif disebut fungsi rasional bilaf(x) dapat dinyatakan sebagai hasil bagi dua fungsi polinomial, yaitu

dengan P(x) dan Q(x) fungsi-fungsi polinomial. Daerah dan wilayah fungsi rasional adalah:

sehingga

untuk

Fungsi Akar Kuadrat
Suatu fungsi f disebut sebagai fungsi akar kuadrat bila memiliki bentuk

Secara umum

Daerah dan wilayah fungsi akar kuadrat adalah:

dan

Fungsi Nilai Mutlak
Fungsi nilai mutlak dinyatakan sebagai : dengan dengan Secara umum :

Operasi pada Fungsi
Misalkan fungsi dan berturut-turut didefinisikan pada daerah dan dan suatu konstanta. Maka : dan merupakan fungsi yang didefinisikan sebagai :
dengan
dengan
dengan
dengan dan
Fungsi Komposisi
Misalkan fungsi dan berturut-turut didefinsikan pada dan Fungsi komposisi didefinisikan sebagai dengan dan